I read somewhere recently – as you approach the real axis of the Mandelbrot set near -0.75 (seahorse valley), the number of iterations before a point escapes, multiplied by the distance to the axis, approaches pi.
It’s a cool fact about the Mandelbrot set. but it isn’t a practical way to calculate pi; it takes a 2*10^n calculations to calculate n digits.

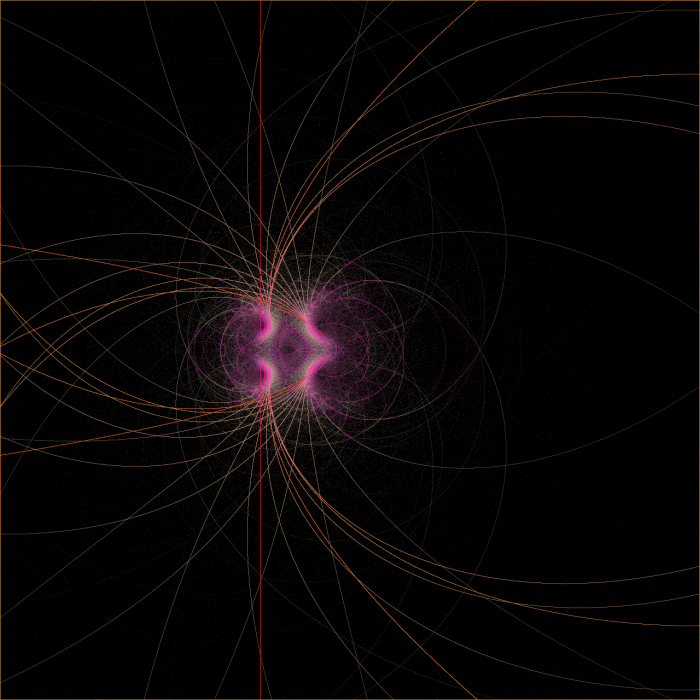
I wanted to know what points in the Mandelbrot set actually did in this area. So I rendered a Buddhabrot with starting points placed along a vertical slice at -0.75:

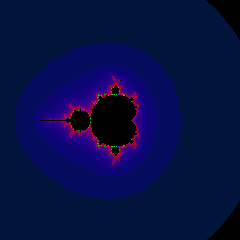
This is zoomed out a ways. Here’s the Mandelbrot set at the same zoom level for reference:

Each line represents a common iteration level for the points of the starting line. each line is completely continuous, because the input function is continuous and the iterated function is too.

As soon as I saw this, I decided to do vertical slices of the entire set.

In the following images,

• The blue channel indicates how close to the real axis a point started. The bluer it appears, the smaller the imaginary component of c is.
• The green channel indicates how far a point has moved through it’s lifetime. If a point takes 500 iterations to escape, it will be drawn with 80% green channel brightness on its 400th iteration.
• The red channel is the reference for the others – it is simply brighter when a pixel is visited more often, and represents the highest value any of the other channels could be for that pixel. (At rasterization time, other channels are multiplied by red and divided by 255.)

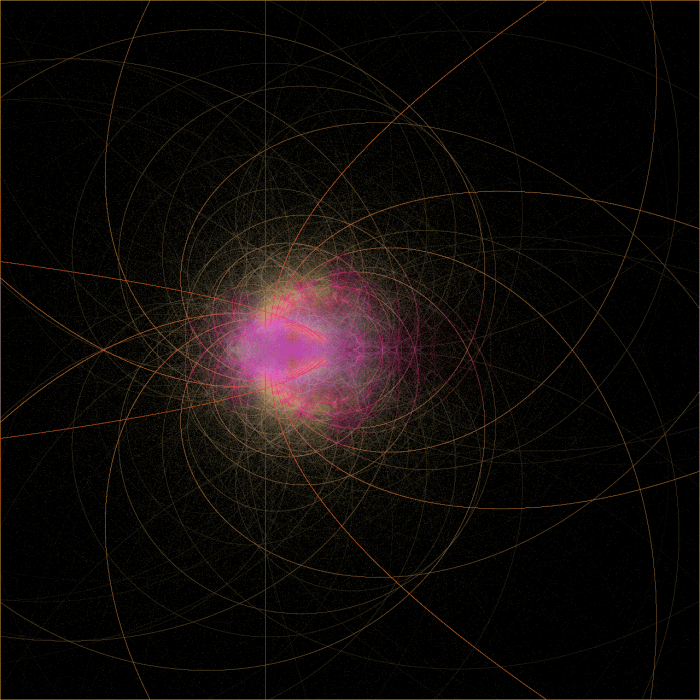
This sequence could be turned into an animation, but it’s quite large for a gif, So I’m looking to post it in a video. I also have several other discoveries to write about soon.